Stones & Measures

To test our ability or desire to impose order on continuous quantity, we gathered a random selection of 300 stones of various sizes. We threw them in a heap on the sand.

We looked at the heap of different stones and considered if they were all different sizes. Even though we knew they were all different, there did seem to be a group that stood out as being the largest stones. We removed these quickly and without too much thought.

No sooner than this was done, another group of the largest stones appeared. We removed these and placed them along the side of the bunch. We repeated the exercise until the whole heap was sorted into seven bundles. 

We repeated the exercise on numerous occasions over a twenty year period with different people. The consistency in the groupings may be seen as our inherent desire to break down continuous quantity into groups of size.

We understand this to be an expression of our intellect, which is to simplify what is beyond our comprehension. We reduced the bundle to 36 carefully graded stones from small to large. We worked the test again.

Immediately, the largest type of size appeared and was immediately removed. The exercise was repeated until the 36 were sorted.

A pattern seemed to emerge that suggested the limits of people’s capacity to deal with continuous quantity. Continuous quantity as presented to us in nature was naturally broken down into 7 sizes: smallest, very small, small, medium, large, larger, largest.

There was debate as to the home of the smallest and largest in each group. The debate covered the stones that occupied the boundaries and limits of the groupings.

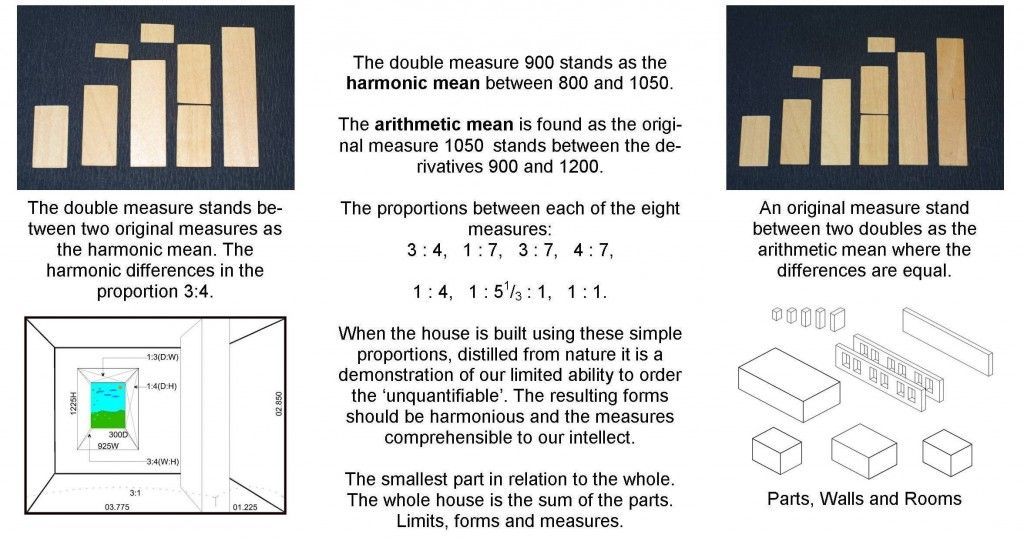
The original experiments undertaken by the Benedictine monks showed that the difference in size between corresponding stones in each group was in the ratio 3:4.

Handmade white cubes provided a vehicle for further experiment. The results however were not as convincing or accurate in the resulting proportions. This was because each consecutive block we made was not 1/24th larger than the previous one.

The ratio 3:4 produces a geometric series very similar to the Fibonacci series. This new series, christened the ‘plastic number’ is slower and described as A+B=D. The reason we think it is slower is due to the 3rd dimension in our experimental materials. The Fibonacci or Golden series (A+B=C) is based on the division of a 2D shape.

We experience built form in 3D. Therefore, we believe the lines and surfaces that generate the form should come under the spell of the plastic number measures and ratios.